In this article I will go over several common shapes in 2 dimensions and investigate how we can test a pair of them for intersection. We will also discuss a general method for testing shapes of a certain class.
Responding to the intersections (and finding them fast) is beyond the scope of this article. This article is concerned only with checking for intersection but is still a pretty large subject.
If you're a little shaky on your mathematics, then I suggest that you refresh yourself thoroughly at least. A good understanding of high school math as well as a lot of college level stuff is integral in the development of games. There's no way around it.
That said, I am not trying to scare you so I will try to be as gentle as possible. The more you do it the easier it gets.
We'll go over the 2D shapes covered briefly then investigate how to test for an intersection between pairs of them.
The Circle
A circle is the set of points in the plane that are the same distance from a common point called its center. This distance from a point in the set to the center is its radius.
We can denote the center of a circle by a point in space with its x and y values, or by a vector and its radius by a real number. Although we'll be working with floats or doubles instead of the infinitude of the reals.
Now we can represent a circle by the equation:
$(x-c_x)^2+(y-c_y)^2=r^2$
Where,
$C = (c_x, c_y)$
is the circle's center point with its x and y components and r is the radius.Every pair of reals, x and y that satisfy this equation for a given real number, r and a point C, is a point on the (unique) circle of radius, r centered at, C.
We can represent a circle simply by storing its position and radius into memory.
class Circle
{
public Vector2 Center;
public float Radius;
}
Rectangle
We'll be dealing with two kinds of rectangles here, axis-aligned, often called bounding boxes and non-axis-aligned. When we're referring to the axis-aligned situation we'll specifically say so, otherwise we'll just say 'rectangle' or 'box'.
Axis-aligned boxes have each of their edges parallel to the coordinate axis while the regular boxes do not.
The built-in Rectangle structure that comes with XNA is axis-aligned.
Many calculations become much simpler when we're dealing with rectangles that are axis-aligned but we'll be looking at both cases.
An axis-aligned box simply has a location (usually referring to the upper-left corner), a width and a height. No other information is needed to describe the bounding box.
class AxisAlignedBox
{
public Vector2 Position;
public float Width;
public float Height;
}
In the other case we need to store a position, a width, a height and an angle of rotation.Here, P is the position and,
$\theta$
(pronounced 'theta') is the angle. A positive angle is measured counter-clockwise.In XNA, by default the origin is the upper-left hand corner of the sprite we're rotating but we'll normally be rotating a box about it's center or perhaps it's center of mass. We'll see how to deal with these things later on.
Other Polygons
There are many different polygons and the only ones we'll look at in any depth are the convex polygons. This is where it get very complicated very quickly and we'll briefly discuss a general method of testing.
Circle-circle test
Two circles in the plane don't intersect if the distance between their centers is greater than the sum of their radii. That is,
$d(c1, c2) = \sqrt{(c1_x-c2_x)^2+(c1_y-c2_y)^2} > r1+r2$
d(c1, c2) is the distance between the centers and c1 and c2 are the centers subscripted by their x or y component.
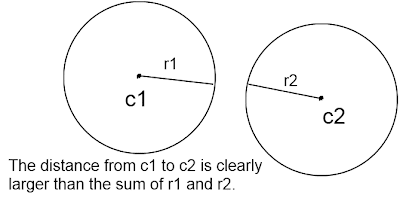 |
| The distance from center to center is larger than their combined radii. No intersection. |
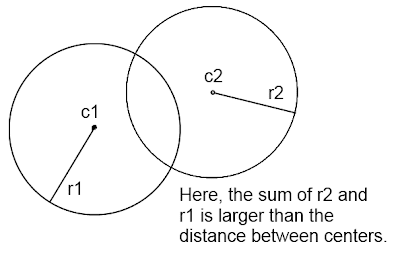 |
| The distance between their centers is smaller than the sum of their radii, hence, they intersect. |
To avoid expensive square root computations we usually compare the square of the distance to the square of the sum of the radii since the inequality remains true.
$(c1_x-c2_x)^2+(c1_y-c2_y)^2 >(r1+r2)^2$
the above is true if the circles don't touch.Adding this to our Circle class,
class Circle
{
public Vector2 Center;
public float Radius;
//Returns true if this circle intersects another
//or they are 'just touching'.
public bool Intersects(Circle circle)
{
Vector2 center1 = Center;
Vector2 center2 = circle.Center;
float radius1 = Radius;
float radius2 = circle.Radius;
float distanceSquared =
(float)Math.Pow((center1.X - center2.X), 2) +
(float)Math.Pow((center1.Y - center2.Y), 2);
float sumOfRadiiSquared = (float)Math.Pow(radius1 + radius2, 2);
if (distanceSquared <= sumOfRadiiSquared)
{
return true;
}
else
{
return false;
}
}
}
Box-box test (axis aligned)
The test for two axis-aligned boxes is fairly straight forward. We'll need to add a few properties to our class first though,
class AxisAlignedBox
{
public Vector2 Position;
public float Width;
public float Height;
//y value of uppermost side.
public float Top
{
get { return Position.Y; }
}
//y value of lowest side.
public float Bottom
{
get { return Position.Y + Height; }
}
//x value of left most side.
public float Left
{
get { return Position.X; }
}
//x value of right most side.
public float Right
{
get { return Position.X + Width; }
}
}
The basic idea is that is if the rectangles intersect, then the top side of one (or the bottom side) will be within the bounds set by the top and bottom sides of the other rectangle. Likewise the left side of one (or the right side) will be within the bounds set by the left and right sides of the other rectangle.Take a look at this picture.
The bottom side of A is below the top side of R and above the bottom side of R, ie. the bottom side of A is within the bounds set by the top and bottom sides of R. Both the left and right sides of A are within the left-right bounds of R. Even though the top side of A is not within the top-bottom bounds, it still intersects.
For B, the top side is within the top and bottom bounds of R and the left side is within R's left and right bounds.
C, while its right side is within the left-right bounds of R, neither it's top nor its bottom sides are within the proper top-bottom bounds of R and it doesn't intersect.
Take a look at the follow case, though.
Rectangle D clearly intersects, but neither it's top nor bottom is within the top-bottom range of R. However, both the top and bottom of R are in D's top-bottom range.
So, roughly in logical terms,
(bottom OR top is within top-bottom bounds of one OR the same with the other) AND
(left OR right is within left-right bounds of one OR the same with the other).
We're pretty much ready to write our algorithm.
class AxisAlignedBox
{
public Vector2 Position;
public float Width;
public float Height;
//y value of uppermost side.
public float Top
{
get { return Position.Y; }
}
//y value of lowest side.
public float Bottom
{
get { return Position.Y + Height; }
}
//x value of left most side.
public float Left
{
get { return Position.X; }
}
//x value of right most side.
public float Right
{
get { return Position.X + Width; }
}
public bool Intersects(AxisAlignedBox box)
{
bool areBottomsInBounds =
(Bottom >= box.Top && Bottom <= box.Bottom) ||
(box.Bottom >= Top && box.Bottom <= Bottom);
bool areTopsInBounds =
(Top >= box.Top && Top <= box.Bottom) ||
(box.Top >= Top && box.Top <= Bottom);
bool areLeftsInBounds =
(Left >= box.Left && Left <= box.Right) ||
(box.Left >= Left && box.Right <= Right);
bool areRightsInBounds =
(Right >= box.Left && Right <= box.Right) ||
(box.Right >= Left && box.Right <= Right);
bool intersects = (areBottomsInBounds || areTopsInBounds) &&
(areLeftsInBounds || areRightsInBounds);
return intersects;
}
}
Another, way to do this which will also be enlightening later on is to note that for rectangle A in the above illustration, the distance from the top of A to the bottom of R is less than the sum of the height of A and the height of R, while at the same time, the distance between the left of A and the right of R is less than the sum of the width of A and width of R. In general, the distance between the uppermost and lowermost points is less than the sum of the heights and the distance between the leftmost and rightmost points is less than the sum of the widths.The code for the other method,
class AxisAlignedBox
{
public Vector2 Position;
public float Width;
public float Height;
//y value of uppermost side.
public float Top
{
get { return Position.Y; }
}
//y value of lowest side.
public float Bottom
{
get { return Position.Y + Height; }
}
//x value of left most side.
public float Left
{
get { return Position.X; }
}
//x value of right most side.
public float Right
{
get { return Position.X + Width; }
}
public bool Intersects(AxisAlignedBox box)
{
//The nested Max calls find the maximum of four different values.
//Similarly with the nested Min values we find the minimum of more than two values.
float horizontalDistance = Math.Max(Right,
Math.Max(box.Right,
Math.Max(Left, box.Left))) -
Math.Min(Right,
Math.Min(box.Right,
Math.Min(Left, box.Left)));
float verticalDistance = Math.Max(Top,
Math.Max(box.Top,
Math.Max(Bottom, box.Bottom))) -
Math.Min(Top,
Math.Min(box.Top,
Math.Min(Bottom, box.Bottom)));
bool intersects = (float)Math.Abs(horizontalDistance) <= Width + box.Width &&
(float)Math.Abs(verticalDistance) <= Height + box.Height
return intersects;
}
}
Box-box test (general)
Before continuing further we need to talk about an important mathematical theorem called the separating axis theorem. We've already used a result of this theorem in the last example and it will end up being the basis for many other intersection problems in the future. We'll go into the theorem in some depth, what it implies and how we can use it to test for intersections.The Separating Axis Theorem
The separating axis theorem states that two convex polygons do not intersect if and only if there exists a line such that when we project the shapes onto that line, the projections do not overlap. The line we project onto is called the axis of separation.
First let's clear up the term "projection onto a line".
The term, projection seems a little overloaded with definitions but they are all closely related.
In our case, we can say informally that we're 'casting a shadow' of the object onto a line.
This picture illustrates three shapes being projected onto an arbitrary line, the x-axis and the y axis.
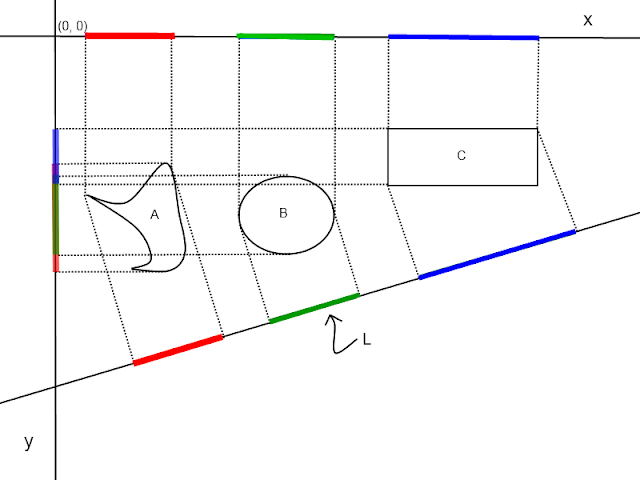 |
| Here we see three shapes being projected onto three lines: The x and y axis and an arbitrary line, L. |
None of these shapes intersect so according to the theorem, there exists a line such that the shapes projections onto that line are separate. Here we see two: the x-axis and the line, L.
This theorem says a lot about when shapes don't intersect but what can we say about when they do? Well, we simply have to negate the theorem to see that two convex polygons intersect if and only if there does not exit a line with said properties. That is, no matter how many lines you project your polyhedra onto, the projections will always overlap.
This poses a problem since there are infinitely many lines we could check.
Luckily in the case of convex polygons there are only a few axis we need to check.
Notice in the axis-aligned box-box method, we only checked the projections of two lines: the x and the y axis. Since both boxes were aligned to those axis those were the only two we had to check.
For a convex polygon, it is sufficient to check the shapes against the axis determined by the normals of each edge (source). If we come across projections that don't overlap we have an early out which will speed up the calculation and if we get through them all and all the projections overlap, then the shapes intersect.
Once we have projections (or the length of them) we can check to see if they overlap similarly to the axis aligned case above.
Before we checked the total distance between the uppermost or lowermost points against the sum of the widths or heights depending.
Now we're checking the distance between the extreme points of the projections along the axis and testing that against the sum of the lengths of the projections. But how do we project these polygons against an axis and find these lengths to begin with?
To start, we'll need to know about vector projection.
The projection of $\bar{a}$ onto $\bar{b}$ is,
$(\bar{a}\cdot\bar{b})\bar{b}=(|\bar{a}|\cos{\theta})\bar{b}$
This can be thought of as the "$\bar{b}$ component of $\bar{a}$". It's in the direction of $\bar{b}$ with a magnitude that varies between $|\bar{a}|$ (when $\bar{a}$ is parallel to $\bar{b}$) and 0 (when $\bar{a}$ is normal to $\bar{b}$).
We also need to tweak our Box class a bit. A lot of the math becomes easier when we keep track of the box's center, its half-height and its half-width. These are similar to a circle's radius except they're vector quantities.class Box
{
//Pseudo-code...
public Vector2 Center;
public Vector2 HalfHeight;
public Vector2 HalfWidth;
public float Angle;
}
Now to measure a projection along a certain axis, take a look at the following illustration,The half-width and half-height projections give us a handy way to measure a shape along an axis. As for the total distance we need only to project the distance between centers onto the axis and find that length. This give us half the total distance. So we can check the length of the projected vectors against that.
To sum up the algorithm we've been piecing together so far:
1. Get the normals of each box, removing duplicates and normals in the opposite direction.
For each normal:
2. Project both of the boxes' half-widths and half-heights onto it and find the sum of their lengths (note: not the length of their sum, since the projections point in opposite directions they tend to cancel eachother). We'll call these H1 and H2 for each box.
3. Project the difference vector of the boxes' centers onto the normal and find its length, we'll call it D.
4. if D > H1 + H2, then there's no overlap, hence no intersection. Otherwise:
5. if there's more normals get the next normal and repeat. Otherwise, all projections overlap and we have an intersection!
And now we're ready to take a look at our new Box class with the interection method.
class Box
{
public Vector2 Center;
//We store these as floats for now,
//we only need the vector versions during
//intersection testing.
public float HalfWidth;
public float HalfHeight;
public float Angle;
public bool Intersects(Box box)
{
//Transform the half measures
Vector2 halfWidthVectOne = Vector2.Transform(
HalfWidth * Vector2.UnitX, Matrix.CreateRotationZ(Angle));
Vector2 halfHeightVectOne = Vector2.Transform(
HalfHeight * Vector2.UnitY, Matrix.CreateRotationZ(Angle));
Vector2 halfWidthVectTwo = Vector2.Transform(
box.HalfWidth * Vector2.UnitX, Matrix.CreateRotationZ(box.Angle));
Vector2 halfHeightVectTwo = Vector2.Transform(
box.HalfHeight * Vector2.UnitY, Matrix.CreateRotationZ(box.Angle));
//They'll work as normals too.
Vector2[] normals = new Vector2[4];
normals[0] = halfWidthVectOne;
normals[1] = halfWidthVectTwo;
normals[2] = halfHeightVectOne;
normals[3] = halfHeightVectTwo;
for (int i = 0; i < 4; i++)
{
normals[i].Normalize();
//Project the half measures onto the normal...
Vector2 projectedHWOne =
Vector2.Dot(halfWidthVectOne, normals[i]) * normals[i];
Vector2 projectedHHOne =
Vector2.Dot(halfHeightVectOne, normals[i]) * normals[i];
Vector2 projectedHWTwo =
Vector2.Dot(halfWidthVectTwo, normals[i]) * normals[i];
Vector2 projectedHHTwo =
Vector2.Dot(halfHeightVectTwo, normals[i]) * normals[i];
//Calculate the half lengths along the separation axis.
float halfLengthOne = projectedHWOne.Length() + projectedHHOne.Length();
float halfLengthTwo = projectedHWTwo.Length() + projectedHHTwo.Length();
//Find the distance between object centers along the separation axis.
Vector2 difference = (Center - box.Center);
Vector2 projectedDiff =
Vector2.Dot(difference, normals[i]) * normals[i];
float projectedDistance = projectedDiff.Length();
//Test for early out.
if (projectedDistance > halfLengthOne + halfLengthTwo)
{
return false;
}
}
//We tested every normal axis,
//we must be in intersection!
return true;
}
}
This test secretly assumes that the rotation is about the center point. Otherwise, we'd need to transform the centers to account for the rotation about a different point. If we were dealing with an origin that was located in the upper-left corner of the box, for example, we'd translate the position by the rotated half-measures to get the correct center.
Also, while we were able to remove a few normals because we knew they were boxes (the ones in the opposite direction as another), we did not go through and test for duplicates. For larger polygons with more normals it may be faster to filter out the duplicate normals.
Circle-box test
For convex polygons there are a finite, if not very large number of normals to check. For a circle one could say there are an infinite amount of normals to check. On the plus side, if we can find a sufficient amount of normals to check, the projection is always the same. Using the same source, we're going to implement the 'naive' axis test where we test against every axis determined by the circles center and a vertex on the box. Ideally we would only need to check against the one determined by the closest vertex. Adding a new method to our Box class,
public bool Intersects(Circle circle)
{
//Transform the half measures
Vector2 halfWidthVect = Vector2.Transform(
HalfWidth * Vector2.UnitX, Matrix.CreateRotationZ(Angle));
Vector2 halfHeightVect = Vector2.Transform(
HalfHeight * Vector2.UnitY, Matrix.CreateRotationZ(Angle));
Vector2[] normals = new Vector2[6];
normals[0] = halfHeightVect;
normals[1] = halfWidthVect;
normals[2] = circle.Center - (Center + halfHeightVect);
normals[3] = circle.Center - (Center - halfHeightVect);
normals[4] = circle.Center - (Center + halfWidthVect);
normals[5] = circle.Center - (Center - halfWidthVect);
for (int i = 0; i < 6; i++)
{
normals[i].Normalize();
Vector2 projectedHalfWidth =
Vector2.Dot(halfWidthVect, normals[i]) * normals[i];
Vector2 projectedHalfHeight =
Vector2.Dot(halfHeightVect, normals[i]) * normals[i];
float halfLength = projectedHalfHeight.Length() + projectedHalfWidth.Length();
Vector2 difference = Center - circle.Center;
Vector2 projectedDifference =
Vector2.Dot(difference, normals[i]) * normals[i];
float projectedDistance = projectedDifference.Length();
if (projectedDistance > halfLength + circle.Radius)
{
return false;
}
}
return true;
}
I also added a method in the Circle class,
public bool Intersects(Box box)
{
return box.Intersects(this);
}
When I tested this I needed to set the box's origin properly:
protected override void Draw(GameTime gameTime)
{
GraphicsDevice.Clear(Color.CornflowerBlue);
Color color = circle.Intersects(rotatedBoxTwo)||circle.Intersects(rotatedBoxOne) ?
Color.Red : Color.White;
spriteBatch.Begin();
Vector2 scaleOne = new Vector2(
rotatedBoxOne.Width / (float)boxTexture.Width,
rotatedBoxOne.Height / (float)boxTexture.Height);
Vector2 scaleTwo = new Vector2(
rotatedBoxTwo.Width / (float)boxTexture.Width,
rotatedBoxTwo.Height / (float)boxTexture.Height);
float circleScale = 2f* circle.Radius / (float)circleTexture.Width;
//Remembering the origin is in texture coordinates, we must scale it down.
spriteBatch.Draw(
boxTexture,
rotatedBoxOne.Center,
null,
color,
rotatedBoxOne.Angle,
new Vector2(rotatedBoxOne.HalfWidth, rotatedBoxOne.HalfHeight) / scaleOne,
scaleOne,
SpriteEffects.None,
0f);
spriteBatch.Draw(
boxTexture,
rotatedBoxTwo.Center,
null,
color,
rotatedBoxTwo.Angle,
new Vector2(rotatedBoxTwo.HalfWidth, rotatedBoxTwo.HalfHeight) / scaleTwo,
scaleTwo,
SpriteEffects.None,
0f);
spriteBatch.Draw(
circleTexture,
circle.Center,
null,
color,
0f,
new Vector2(circle.Radius, circle.Radius) / circleScale,
circleScale,
SpriteEffects.None,
0f);
spriteBatch.End();
base.Draw(gameTime);
}
I hope this cleared a lot of stuff up about intersections between shapes. Again, if you're intersested, check out this page for more information. There's algorithms about some convex shapes too.
Thanks for reading!








No comments :
Post a Comment